0
  • LOGIN

  • No products in the cart.

SUBMATH: WORK, POWER AND ENERGY

This unit is about work, energy and power
SUBMATH: WORK, POWER AND ENERGY 1

Work is referred to as the displacement of an object when a force (push or pull) is applied to it while energy is referred to as the capacity to do the work. It exists in various forms like potential, kinetic, chemical, thermal, nuclear, electrical energy and so on. Power is the work done per unit of time.

What is Work, Energy and Power?

Work
Definition Work is said to be done when a force applied to an object moves that object.
Formula We can calculate work by multiplying the force by the movement of the object.W = F × d
Unit The SI unit of work is the joule (J)

Energy
Definition In physics, we can define energy as the capacity to do work.
Formula For the potential energy the formula isP.E. = mgh
Unit The SI unit of energy is joules (J), which is named in honour of James Prescott Joule.

Power
Definition Power can be defined as the rate at which work is done i.e. energy converted.
Formula The formula for power isP = W/t
Unit The unit of power is watt (W).

  • Work Done = FD cos (\theta ) where F is the Force applied to an object, D is the distance moved by the object and  \theta   is the angle at which the force is applied.
  • The energy of a body is its capacity for doing work.
    i)  Kinetic\quad Energy\quad =\quad \frac { 1 }{ 2 } \quad m{ v }^{ 2 }
    ii)  Potential\quad Energy\quad =\quad m\quad g\quad h
  • Power is the rate of doing work or the work done per second. The unit of power is the watt.
    Power\quad =\quad Force\quad \times \quad Velocity

Work

When a force is applied to an object and the object covers a certain distance in the direction of the force, then the force is said to do work. The unit of work is called Joules (J). One Joule is defined as the work done by a force of 1 Newton in moving a body a distance of 1 metre in the direction of the force.

For large amount of work, the unit used is KiloJoule (KJ) which is equivalent to 1000 Joules.

Let’s study a few different cases of work:

i)    Let F Newton be a force applied to a body. The body covers a distance of D metres from point A to point B in the direction of the force as shown in Fig 1, then the work done by the force is equal to  F\quad \times \quad D.

ii)   Let’s suppose a force F Newton acts on a body and moves it from point A to B and F makes an angle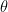  \theta   with the direction of the displacement D.

As shown in Fig 2 , the resolved part of F along AB = F cos (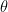\theta ), therefore only F cos (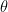\theta ) does the work.

The work done by the force F is =\quad (F\quad cos(\theta ))\quad \times \quad D

Work\quad Done\quad =\quad FD\quad cos(\theta )

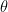iii)   If  \theta   = 90°, i.e the force and the displacements are perpendicular to each other, then the work done by the force is ZERO.

Conversely if the work done by a force F is 0, then F and the displacement are perpendicular to each other.

iv)   If there are different forces, ie p, q, r etc acting on a body, then the work done by these forces in any displacement of the object is equal to the algebraic sum of the work done by p, q , r separately.

Example #1

Q. Leo applies a force of 200 N to a box to move it 5 m forward. The Force applied is inclined upwards by 20°. Find the work done.

Solution:

We know:

Work\quad Done\quad =\quad Force\quad \times \quad Distance

As the force applied has an angle the formula will have cos (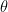\theta )

Work\quad Done\quad =\quad FD\quad cos(\theta )

\theta \quad =\quad 20°

F = 200 N

D = 5 m

Work Done = 200(5) (cos (20))

Work\quad Done\quad =\quad 1000\quad \times \quad 0.939

Work Done 939.7 Joules     Ans

Energy

The energy of a body is its capacity for doing work. The unit of work is Joule. Since energy of a body is measured by the work, therefore unit of energy is also Joule. There are many kinds of energy but in Dynamics, we are concerned with Mechanical energy which deals with kinetic and potential energy only.

spring
A coiled spring has elastic energy.

A battery contains electrical energy. We can drain that energy out to do work.

Fuel contains chemical energy. An engine can turn that fuel (with oxygen) into work, making your car go!

hammer

A hammer has mechanical energy:

  • when raised up it has potential energy (the energy of position)
  • when falling down it has kinetic energy (the energy of motion)
 

Energy goes from one storage to another, or goes to heat:

energy work heat

Heat is a type of energy, too. In fact the total amount of energy stays the same:

Energy can’t be created or destroyed.

Kinetic Energy

Kinetic Energy of a body is measured by the amount of work it does in bringing it from rest to state where its speed is v m/s.

For a body with mass m moving with speed v m/s , the kinetic energy is defined as:

Kinetic\quad Energy\quad =\quad \frac { 1 }{ 2 } \quad m{ v }^{ 2 }

Potential Energy

The potential energy of an object is the energy due to its position with respect to some standard position. The potential energy of an object of mass m at height h above the surface is the work that the object can do in falling to the surface and this is equal to the work done in raising it to the height h.

Potential\quad Energy\quad =\quad m\quad g\quad h

Lastly , we can recall from GCSE’s, law of conservation of energy which states that energy can be transformed from one form to another but it cannot be created or destroyed.

In a case where kinetic energy and potential energy are increasing or decreasing simultaneously then the formula for word done becomes:

Work done by an external Force = Change in PE + Change in KE + Work Done against Friction

Example #2

Q. A load of mass 100 Kg is raised vertically by a crane. During the motion the load passes through the points A and B where B is 1.7 m above A. Its speed at A is 3 m/s and at B is 2 m/s. For the motion from A to B, find:

i) The gain in Gravitational Potential Energy
ii) The loss in Kinetic Energy of the load
iii) The work done by the crane, on the load.

Solution:

We can say that A is the initial point

i) Gain in Gravitational Potential Energy = m g h

=\quad 100\quad \times \quad 10\quad \times \quad 1.7\quad =\quad 1700 Joules

ii) Loss in Kinetic Energy is going from A to B  =\quad \frac { 1 }{ 2 } \quad m{ v }^{ 2 }

=\quad \frac { 1 }{ 2 } \quad \times \quad m{ ({ 3 }^{ 2 }\quad -\quad { 2 }^{ 2 }) }\quad =\quad 250 Joules

iii) Work Done by the crane = Gain in Potential Energy(PE) – Loss in Kinetic Energy(KE)

= 1700 – 250
= 1450 Joules

Power

Power is the rate of doing work or the work done per second. The amount of work done per second, therefore indicates how powerful a machine is. This gives us the concept of power or the rate of doing work.

The unit of power is the ”watt”. It is 1 Joule/second and is written as 1W.

Power\quad =\quad Force\quad \times \quad Velocity

Example #3

Q. A train has a maximum speed of 90 Km/h on the level against a resistance of 60,000 N. find the maximum power of the engine.

Solution:

As it is mentioned that the train is moving at a maximum speed hence we know that acceleration = 0.

Therefore:

Driving Force = Resistance

F = 60,000 N

Power\quad =\quad Force\quad \times \quad Velocity

=\quad 60000\quad \times \quad \frac { 90\quad \quad \times \quad 1000 }{ 60\quad \times \quad 60\quad }

= 1500,000 Watt

= 1500 KW

Same Direction!

The force and movement are measured in the same direction.

Work  =  Force × Distance × cos θ

Where θ is the angle between the force and the direction of motion.

So any force that is sideways to the movement is not included.

Example: John pushes a box 3 m straight forward using 200 N of force. But his push is a little upwards by 20°.

push box 20 degrees

Start with:

Work  = Force × Distance × cos θ

Put in the values we know:

Work  = 200 N × 3 m × cos 20°

Work  = 200 N × 3 m × 0.9397…

Work  = 564 N m (to nearest N m)

1 N m is 1 Joule (J) the preferred unit for work and energy (more on this later):

Work  = 564 J

(Without cos θ, the wrong value would be 600 J)

Here are some other angles:

cos(0°)=1   cos(60°)=0.5   cos(90°)=0
force along distance   force at 60 degrees to distance   force at 90 degrees to distance
W = Fd   W = Fd × 0.5   W = 0

So remember:

  • Without movement there is no work
  • Force and movement in the same direction
  • Work  =  Force × Distance × cos θ

One joule is about:

  • the energy needed to lift an 0.1 kg apple up 1 meter
  • The energy released when the apple falls back down again
  • The heat needed to raise a single drop of water by 5° C
  • 1 watt of electricity for 1 second

And:

  • An LED light uses about 3 J every second
  • A human at rest releases about 60 J of heat every second

Example: How much energy is needed to lift an 0.1 kg apple up 1 meter?

gravity apple force

To hold a 0.1 kg apple against gravity needs 1 Newton of force:

F = mg

F = 0.1 kg × 9.8 m/s2

F ≈ 1 N

But holding an apple is not work, the apple needs to move!

So, raising it using 1 N for 1 m (both in same direction!) gives:

Work  =  1 N × 1 m × cos 0°

= 1 J

A kilojoule (kJ) is 1000 J:

  • A fan heater releases about 2 kJ of heat every second
  • to heat the water for a cup of coffee needs 80 kJ

A Megajoule (MJ) is 1 million J:

  • A 2500 kg car going at highway speed has 1 MJ of energy
  • A big TV uses about 1 MJ of electricity every hour
  • One kW h (kilowatt hour) of electricity is 3.6 MJ
  • A fan heater releases about 8 MJ of heat every hour

A Gigajoule (GJ) is 1 billion J:

  • The solar energy falling on a roof is about 1 GJ to 5 GJ every day
  • A person uses about 20 GJ in their home every year

Efficiency

Efficiency is how much of the energy is useful as a percent of the total energy.

Efficiency = Useful EnergyTotal Energy as a percentage

Example: For every 100 MJ (Megajoule) of energy a gasoline engine uses, only 25 MJ goes to driving it forward.

Efficiency = 25 MJ100 MJ= 25%

Summary

  • Work is force times distance (in the same direction!)
  • W = F d cos θ
  • Energy is the ability to do work
  • Energy goes from one storage to another, or goes to heat
  • Energy can’t be created or destroyed (Conservation of Energy)
  • The basic unit of energy is 1 Joule (J)
  • 1 J = 1 N m

VIDEO TUTORIAL

Assignment

SUBMATH: Work, Power and Energy Assignment

ASSIGNMENT : SUBMATH: Work, Power and Energy Assignment MARKS : 20  DURATION : 1 week, 3 days

 

Courses

Featured Downloads

af Afrikaanssq Albanianam Amharicar Arabichy Armenianaz Azerbaijanieu Basquebe Belarusianbn Bengalibs Bosnianbg Bulgarianca Catalanceb Cebuanony Chichewazh-CN Chinese (Simplified)zh-TW Chinese (Traditional)co Corsicanhr Croatiancs Czechda Danishnl Dutchen Englisheo Esperantoet Estoniantl Filipinofi Finnishfr Frenchfy Frisiangl Galicianka Georgiande Germanel Greekgu Gujaratiht Haitian Creoleha Hausahaw Hawaiianiw Hebrewhi Hindihmn Hmonghu Hungarianis Icelandicig Igboid Indonesianga Irishit Italianja Japanesejw Javanesekn Kannadakk Kazakhkm Khmerko Koreanku Kurdish (Kurmanji)ky Kyrgyzlo Laola Latinlv Latvianlt Lithuanianlb Luxembourgishmk Macedonianmg Malagasyms Malayml Malayalammt Maltesemi Maorimr Marathimn Mongolianmy Myanmar (Burmese)ne Nepalino Norwegianps Pashtofa Persianpl Polishpt Portuguesepa Punjabiro Romanianru Russiansm Samoangd Scottish Gaelicsr Serbianst Sesothosn Shonasd Sindhisi Sinhalask Slovaksl Slovenianso Somalies Spanishsu Sundanesesw Swahilisv Swedishtg Tajikta Tamilte Teluguth Thaitr Turkishuk Ukrainianur Urduuz Uzbekvi Vietnamesecy Welshxh Xhosayi Yiddishyo Yorubazu Zulu
en English